Elipse
- Maria Fernanda Oliveira
- 19 de out. de 2021
- 2 min de leitura
Fixados 2 pontos chamados de focos (F1 e F2) em que a distância entre eles é 2c, elipse é o lugar geométrico de todos os pontos cuja soma da distância de cada ponto a F1 e F2 é maior que 2c e vale 2a.

Observe o comportamento de um ponto da elipse. A soma da distância dele aos focos (S=2a) é sempre constante e maior que 2c (distância entre os focos).
Elementos da elipse

A elipse possui um eixo maior e um menor. A distância do centro ao eixo maior é o valor de a. A distância do centro ao eixo menor é o valor de b.
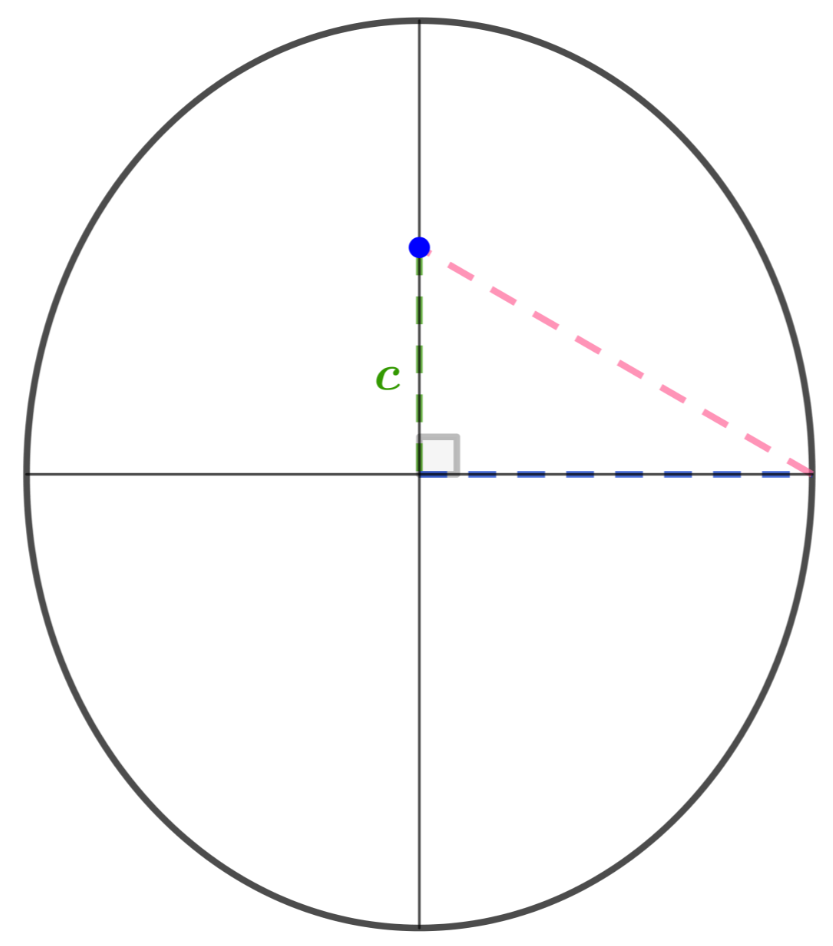
A distância do centro ao foco é c.
A interseção dos eixos em seus pontos médios é o centro da elipse.
Equação da elipse
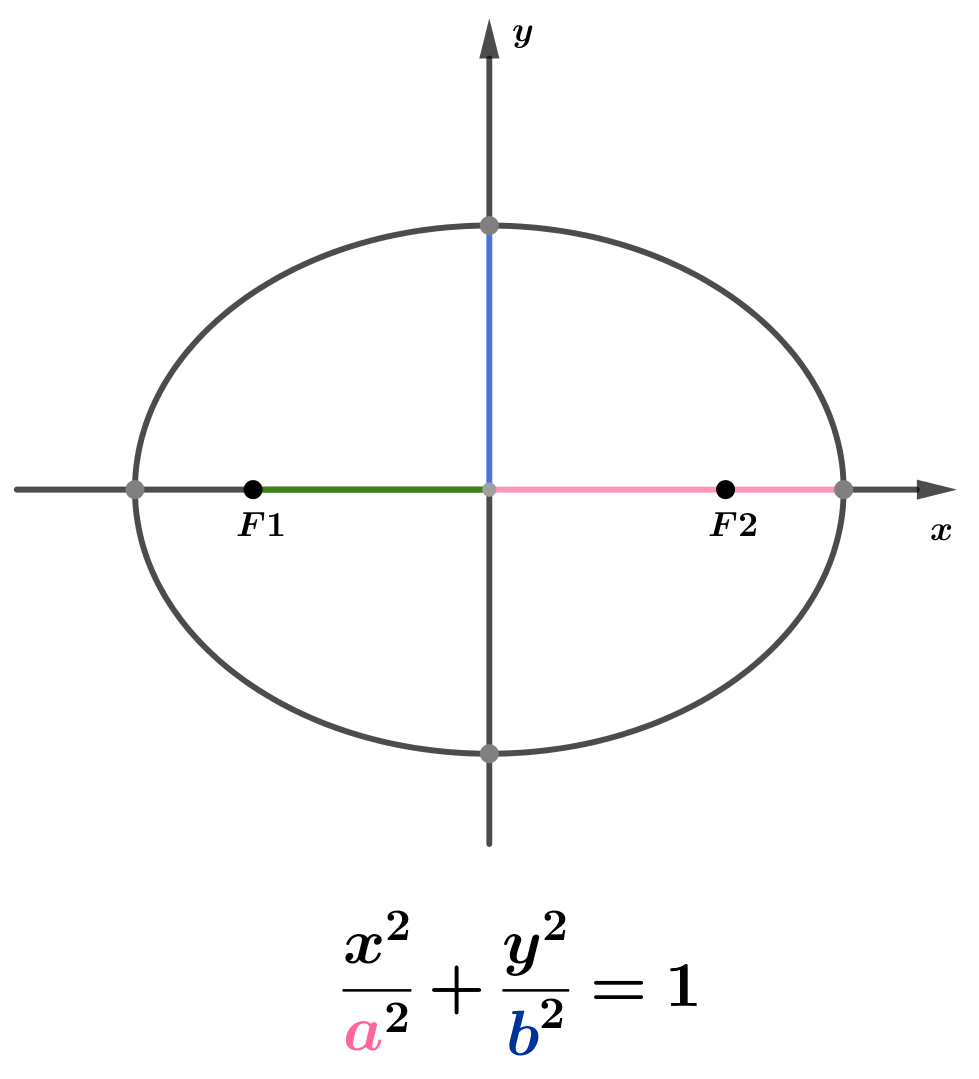
1) Fixando o centro na origem do plano cartesiano

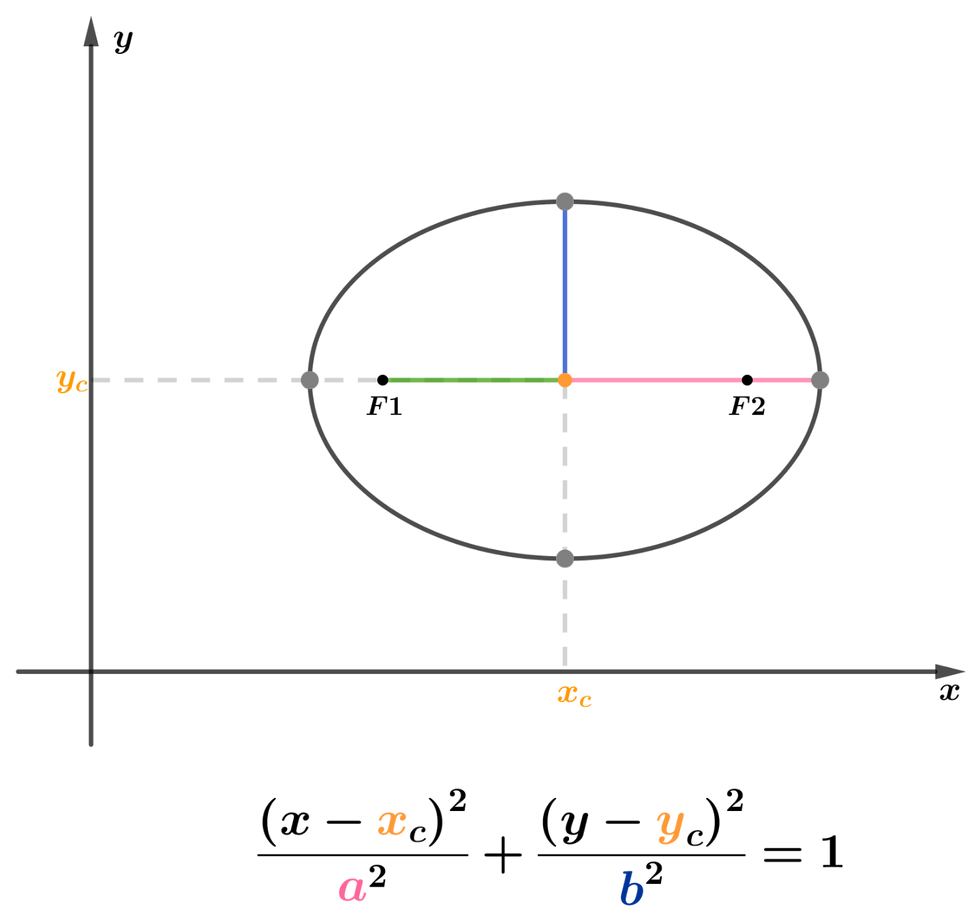
2) Centro fora da origem do plano cartesiano

Observação
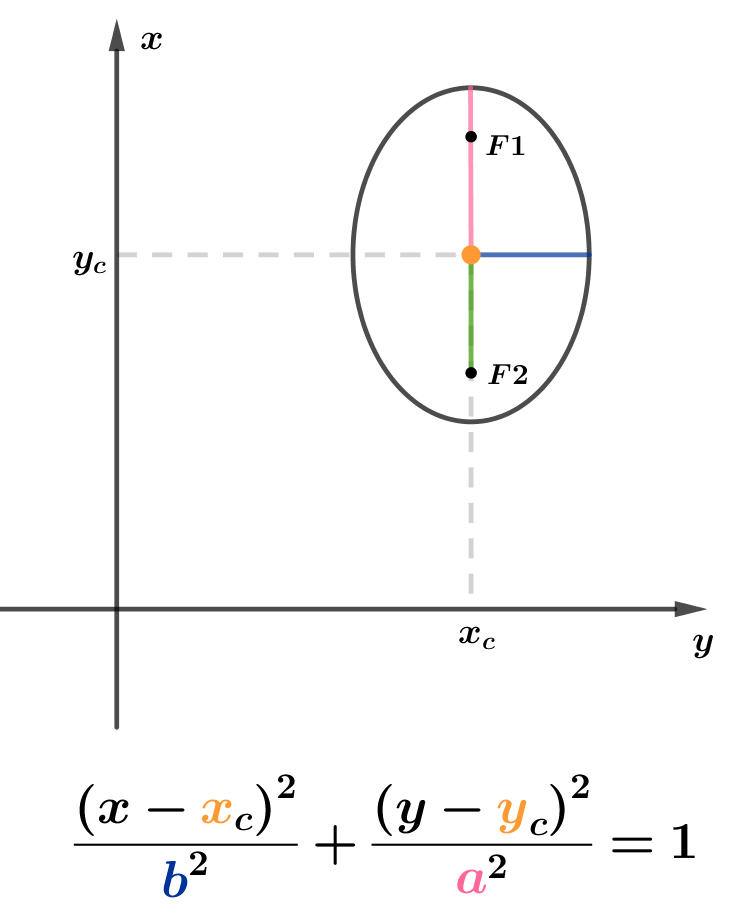
Se os focos da elipse estiverem sobre o eixo y

Observe que neste caso, a (valor maior) fica sob o y², e, de fato, é representada no eixo y ou paralelamente ao eixo y.
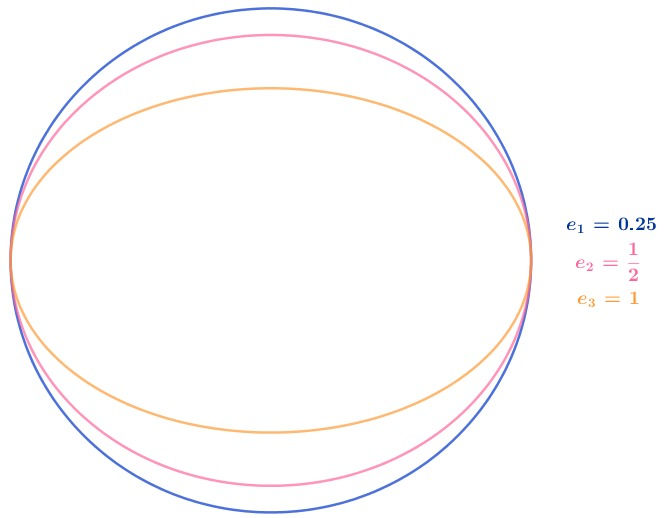
Excentricidade
A excentricidade indica se a elipse é mais ou menos ''achatada''. Quanto maior a excentricidade, mais achatada ela é.


Resumo
 |  |
 |  |
Exercícios
1) Desenhe as elipses
a) x²/9 + y²/4 =1
b) x²/4 + y²/9 =1
c) (x-6)²/3² + (y-7)²/2² =1
Resposta
a) Elipse com centro na origem, a=3 e b=2
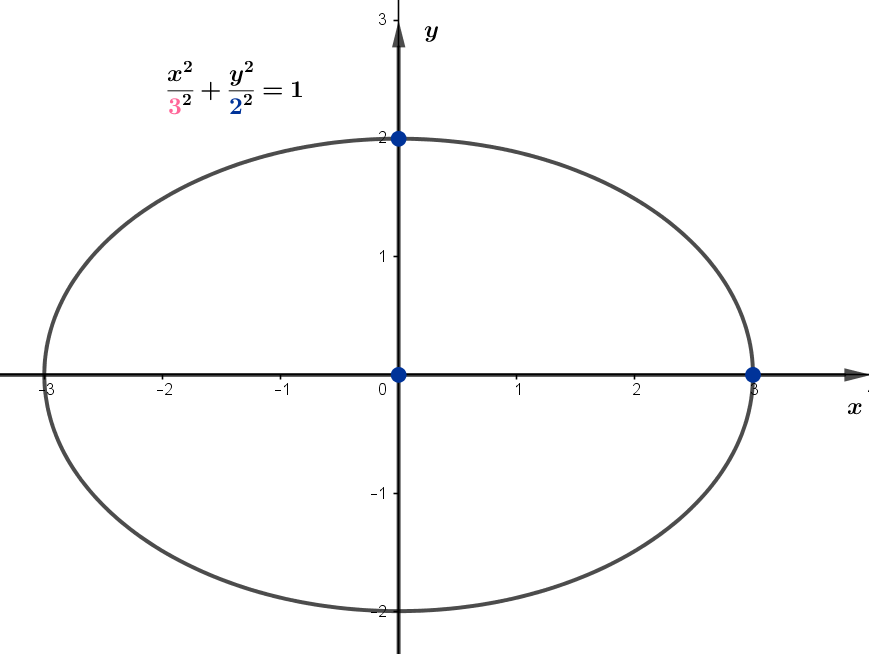
b) Elipse com centro na origem, b=2 no eixo x e a=3 no eixo y.

c) Elipse com centro C(6,7), a=3 e b=2
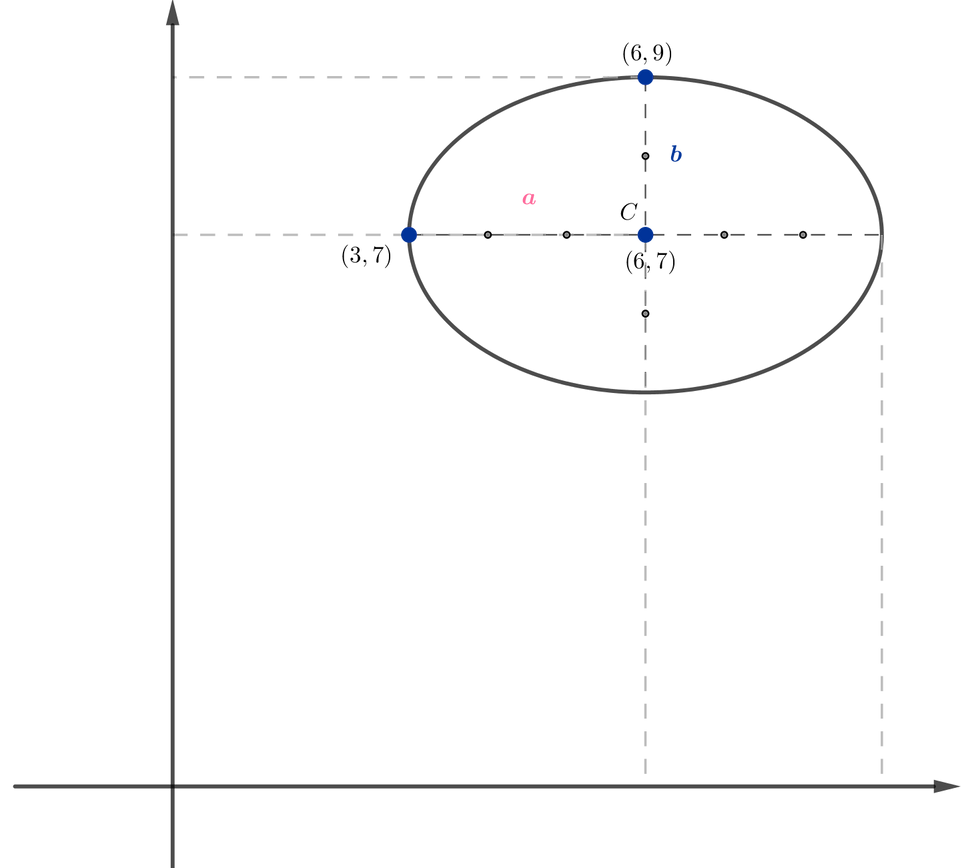
Observação: se quiser descobrir o valor de ''c'', basta calcular:

2) Dê a equação da elipse:

Resposta

3) Qual é o centro da elipse abaixo?

Resposta
O centro tem a mesma ordenada dos focos, então yc=3. xc é o ponto médio de
F1F1: 4-2/2=1, portanto, de xc caminha-se 1 em x, e encontra-se a abscissa do centro.

5) Defina os focos da elipse abaixo

Resposta
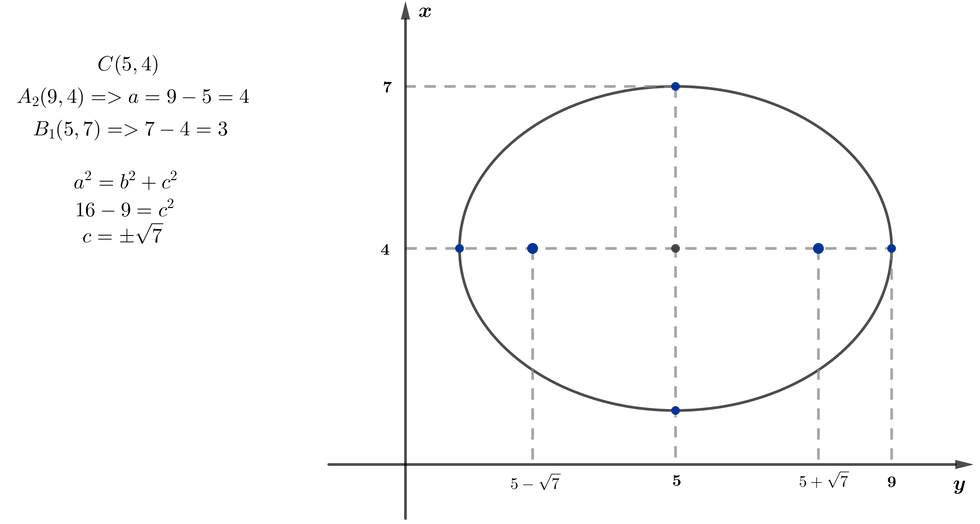
.png)

Comentários